円に内接する四角形ABCDにおいて、 AB=5 BC=3 CD=5 B=120°である時の値を求めよ。(1)AC (2)AD (3)円の半径R (4)△ACDの内接円の半径r

今回の問題

円に内接する四角形ABCDにおいて、 AB=5 BC=3 CD=5 B=120°である時の値を求めよ。
(1)AC　 (2)AD (3)円の半径R　(4)△ACDの内接円の半径r

主に定期テストで問われることが多いタイプの問題です。必ずマスターしましょう！

解答例

まずは図示してみましょう。フリーハンドでなるべく正確に書くとおおよその検討がつくため、練習から丁寧に図を描いてみましょう。

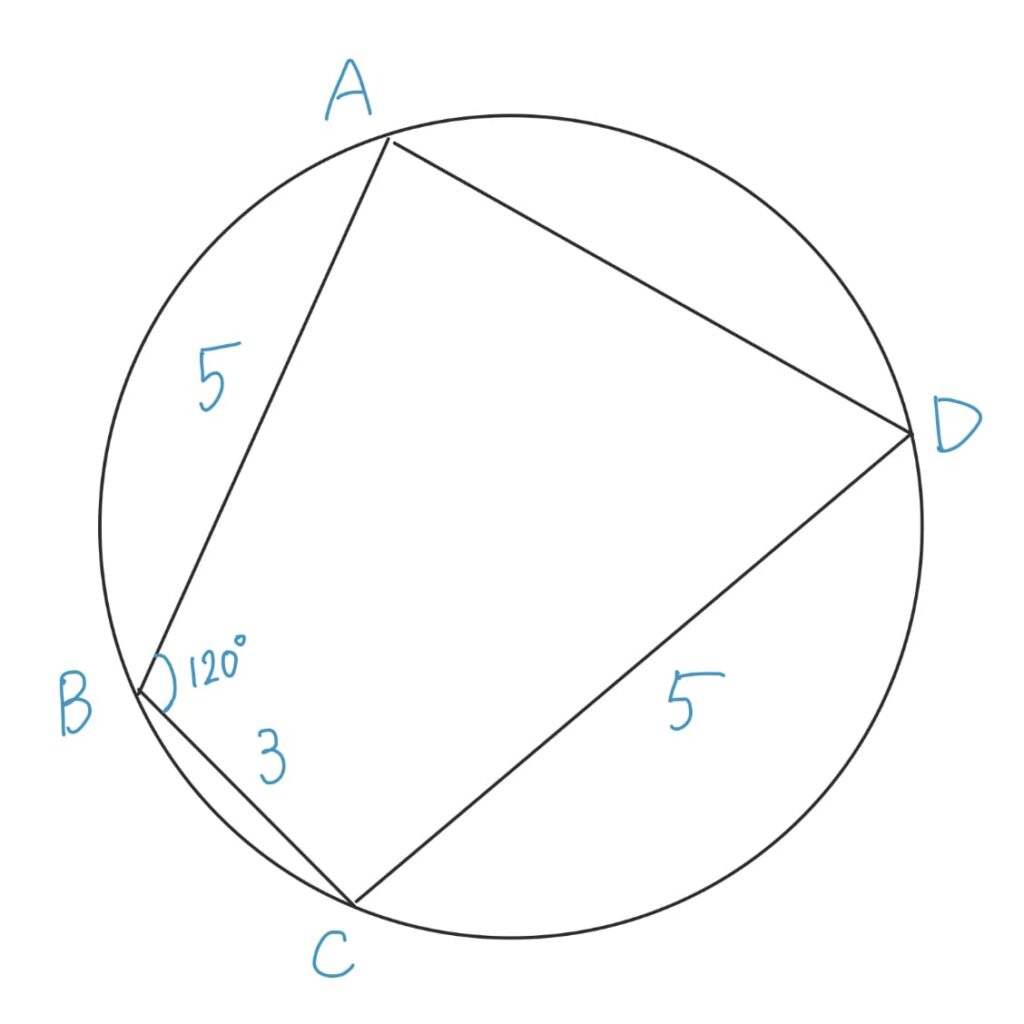
では以降順番に解いていきます。解答に至る発想もご紹介していきます。

(1) ACの大きさ

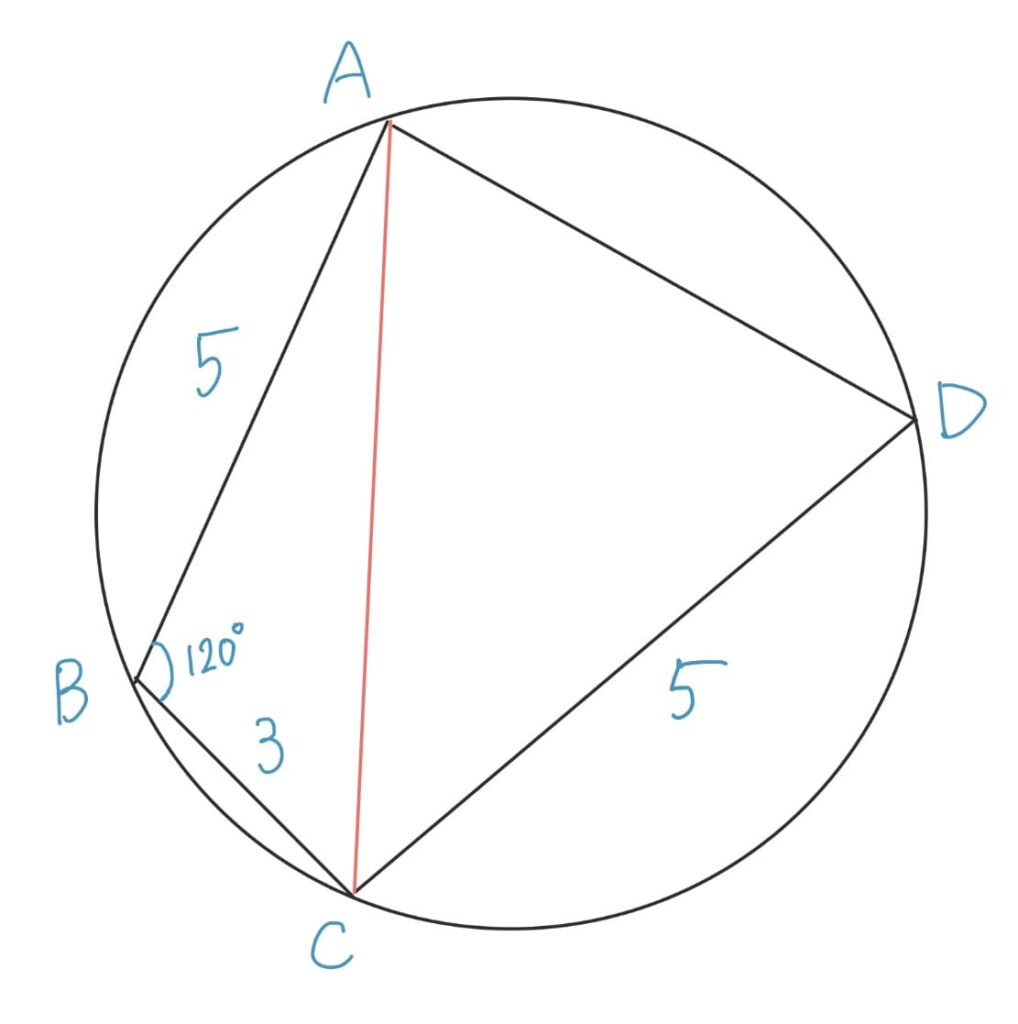
ACはこの四角形の対角線ですのでACを結んでみます。すると△ABCにて余弦定理が使えます。

AC² = 5²+3²-2×5×3×cos120° = 25+9+15 =49

ここでACは辺の長さなので、必ず正になることに注意すると、AC=7 となります。

(2) ADの大きさ

ADを求める前に重要事項を確認しましょう。円に内接する四角形の対角の和は180°になります。とても重要な声質になりますので覚えておきましょう。今回その性質を使うと角ADCは60°になります。（下図）

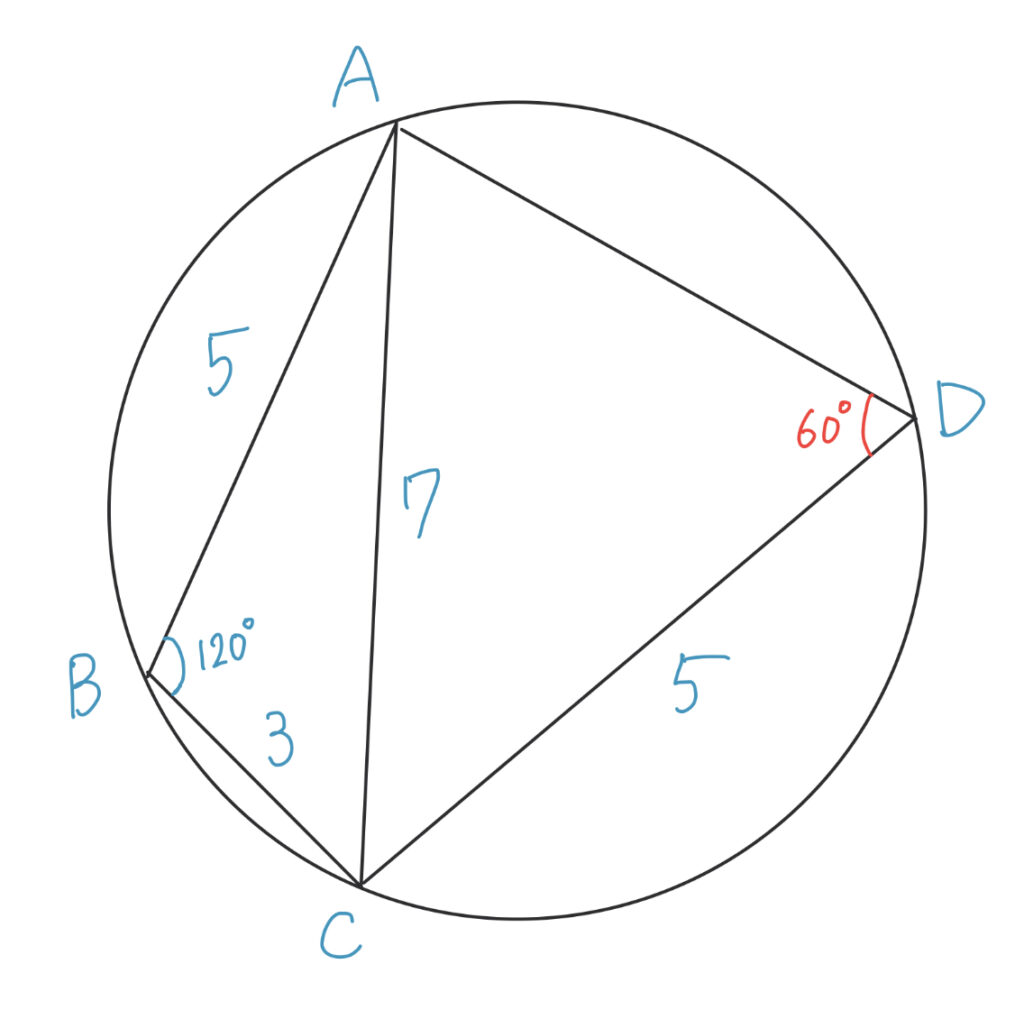
ここで△ACDにて再度余弦定理を使いましょう。

7² = AD²＋5²-2×AD×5×cos60°
49 = AD²＋25-5AD
(AD+3)(AD-8) = 0
ここでAD＞0 ですので AD = 8となります。

(3) 円の半径R

今回のように、三角形に外接する円のことを「外接円」といいます。外接円の半径を求める問題では「正弦定理」を使いましょう。すると計算は以下のようになります。

2R = 7 / sin60°
=14/√3R
=7/√3
=7√3/3

(4) △ACDの内接円の半径r

△ACDの内接円を図にすると以下のようになります。

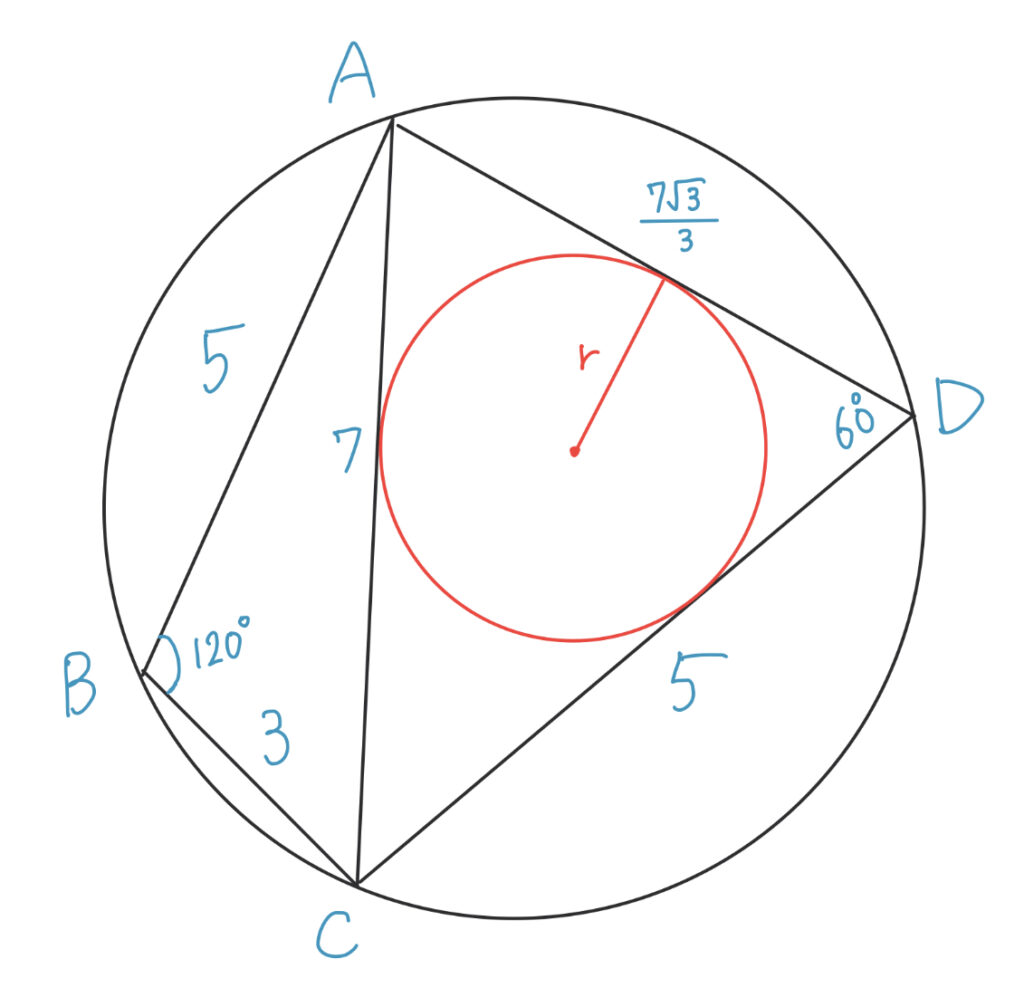
ここで、内接円の半径 r を求める以下の公式があります。三角形の3辺の長さをa, b, c、三角形の面積をSとすると

S=r/2×(a+b+c)

従って、まずは三角形の面積Sを求めます。三角形の面積公式 S=1/2×a×b×sinCを用いると

S (△ACD)
＝ (1/2)×5×8×sin60°
＝ 20×(√3/2)
＝ 10√3 　となります。

次に公式の右辺の計算で面積Sを計算すると

S (△ACD)
＝ (1/2)×r×(7＋8＋5)
＝ 10r　 となります。

この２つは当然同じですのでイコールで結んで答えが得られます。

10r
＝10√3 r
＝√3

まとめ

今回の問題は定期テストで頻出の問題です。どれも重要な問題かつ解法ですので、高校生の皆さんは必ずマスターしておきましょう！

こちらの解説記事もおすすめです！（全て数学ⅠAです）

• 高校入試で使える最強の数学の公式＆裏技10選！！【中学数学＆高校受験】
  受験生の皆さん、勉強… 続きを読む: 高校入試で使える最強の数学の公式＆裏技10選！！【中学数学＆高校受験】
• 【早く簡単に】たすき掛け・因数分解で使える裏技をご紹介します。一瞬で時短＆計算ミスを防げます。【高校数学I】
  この記事は数学１で習… 続きを読む: 【早く簡単に】たすき掛け・因数分解で使える裏技をご紹介します。一瞬で時短＆計算ミスを防げます。【高校数学I】
• メネラウスの定理の簡単な覚え方とポイント！これでもう間違えない！
  多くの方が高校１年生… 続きを読む: メネラウスの定理の簡単な覚え方とポイント！これでもう間違えない！
• チェバの定理の簡単な覚え方とポイント！これでもう間違えない！
  多くの方が高校１年生… 続きを読む: チェバの定理の簡単な覚え方とポイント！これでもう間違えない！
• 【３通りで説明】ｎが自然数（正の整数）ならば、ｎ^5-ｎは３０の倍数であることを示せ。
  今回解説する問題はこ… 続きを読む: 【３通りで説明】ｎが自然数（正の整数）ならば、ｎ^5-ｎは３０の倍数であることを示せ。