練習問題2
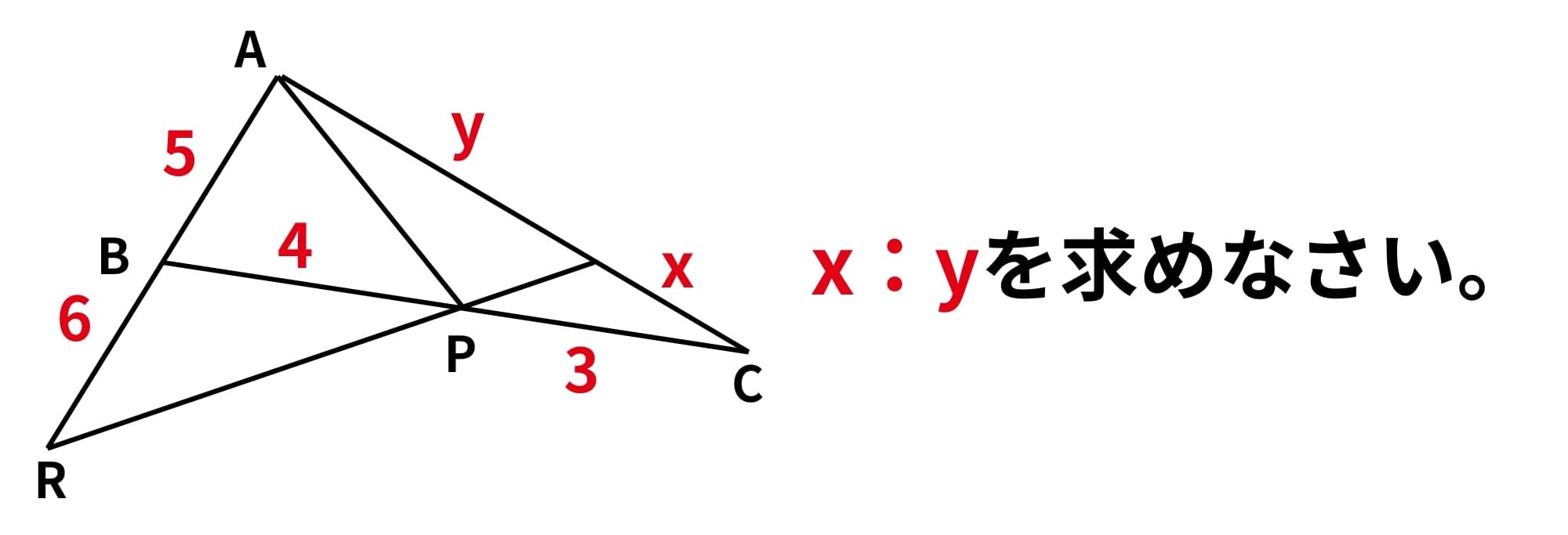
この問題もメネラウスの定理が使えますよ。そこで先ほどの3STEPの出番です。実際にやってみましょう!

チェバじゃないの、、?と思った方はぜひ最後に触れておりますので、ご覧ください!
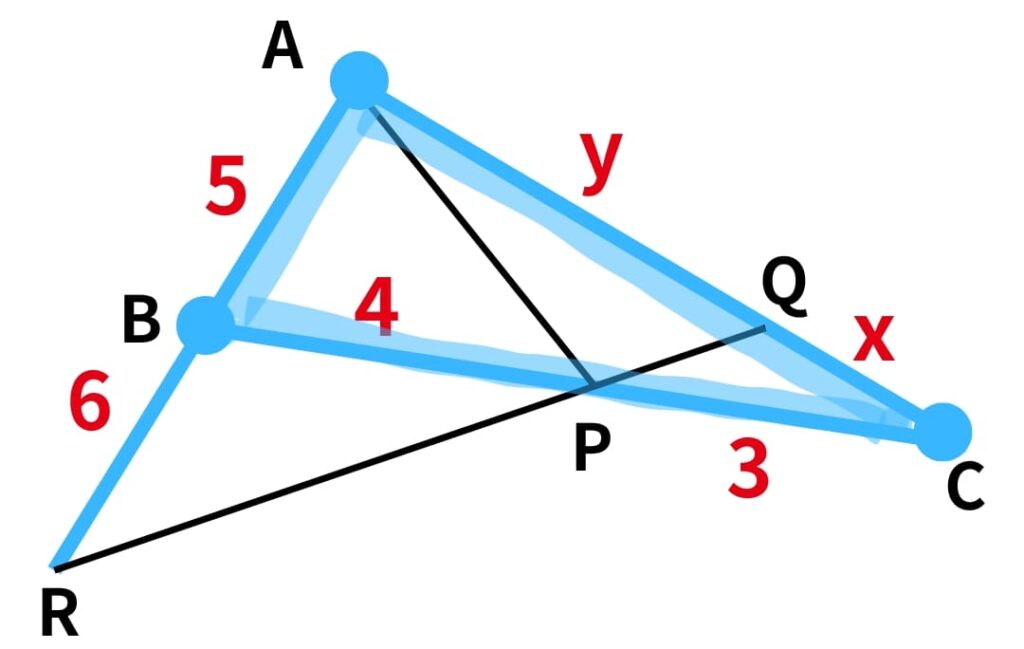

この問題で長さがわかっているところと求めたいxとyの辺を濃くしましょう。AB, BR, BP, PC, CQ, ACを濃くしたらいいですね。
そしたら今描いた線に囲まれた三角形ができますよね。今回も△ABCですね。
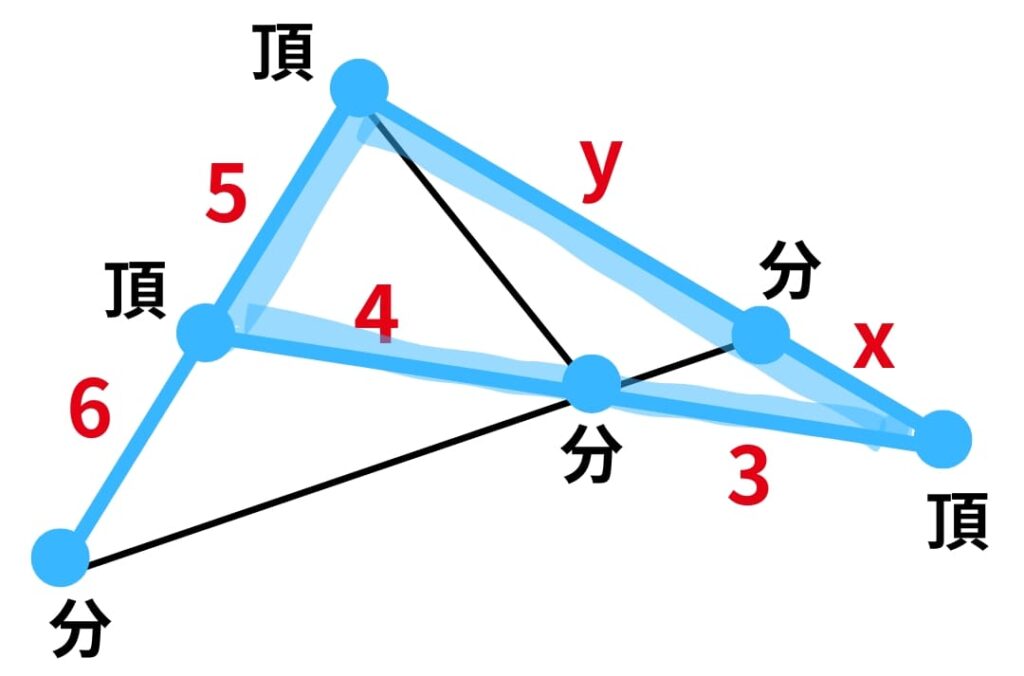

次にSTEP1で出来た三角形の頂点を決めます。今回でいうと頂点はA, B, Cのところです。またそれ以外の点は全部分点になります。
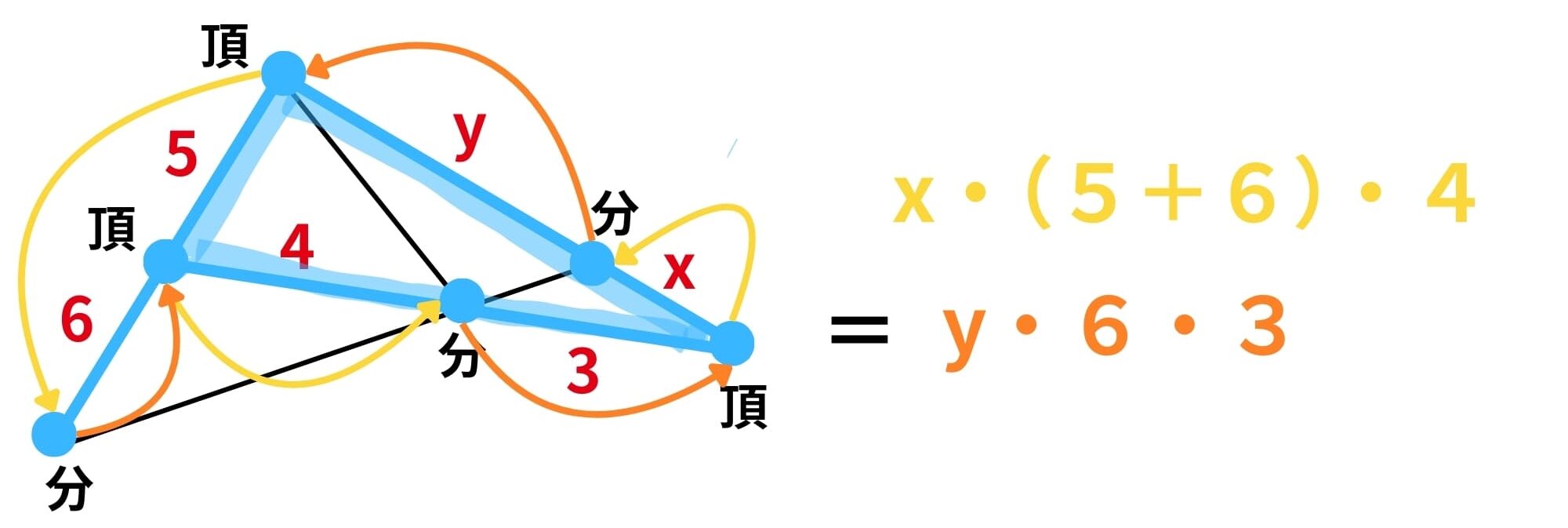

x・(5+6)・4 = y・6・3と左右に分けてかけていきます!



三角形を1周する感覚を覚えておきましょう!
コツは頂点から出た矢印は必ず分点へ、分点からでた矢印は必ず頂点に向かうことです。
以下の計算はこのようになります。確認してみてください。
\begin{eqnarray}
&&x \times (5+6) \times 4 =y \times 6 \times 3 \\
&&44x = 18y\\
&&x:y =18:44\\
&&x:y =9:22\\
\end{eqnarray}
練習問題1と同様に、内項の積=外項の積を考えると分かります。最後の約分も忘れないように注意してください。



これで2パターンどちらも解けましたね!どちらのパターンでも解き方は同じになるので、あとは他に練習問題を解いて確実性を上げていってください!
実はチェバの定理も同じ解き方で可能!
問題を見た時に、チェバを使うのかメネラウスを使うのか、分からないという方がよくいらっしゃいます。しかし実はチェバの定理もメネラウスの定理もどちらも解法は同じなんです。
つまりどちらも今回ご紹介した3STEPで解くことができます。どちらかは分からなくてもいいので、この3ステップを試してみることで得たい比を得ることができますよ。
チェバの定理は下記の記事からぜひご覧ください!


テストなど頑張ってくださいね、応援しています!!!!










コメント