
最終的には「慣れ」が大切なのですが、この方法を知ると少し考えることが少なくなりスピードアップが出来ますよ!
問題
いきなりですが次の式を因数分解してみてください。
\begin{eqnarray}
6x^2+7x+2
\end{eqnarray}
まずは以下のように準備をすると思います。ここで、掛けて2になるのは2×1しかありませんから、真ん中の列は2と1で確定させました。
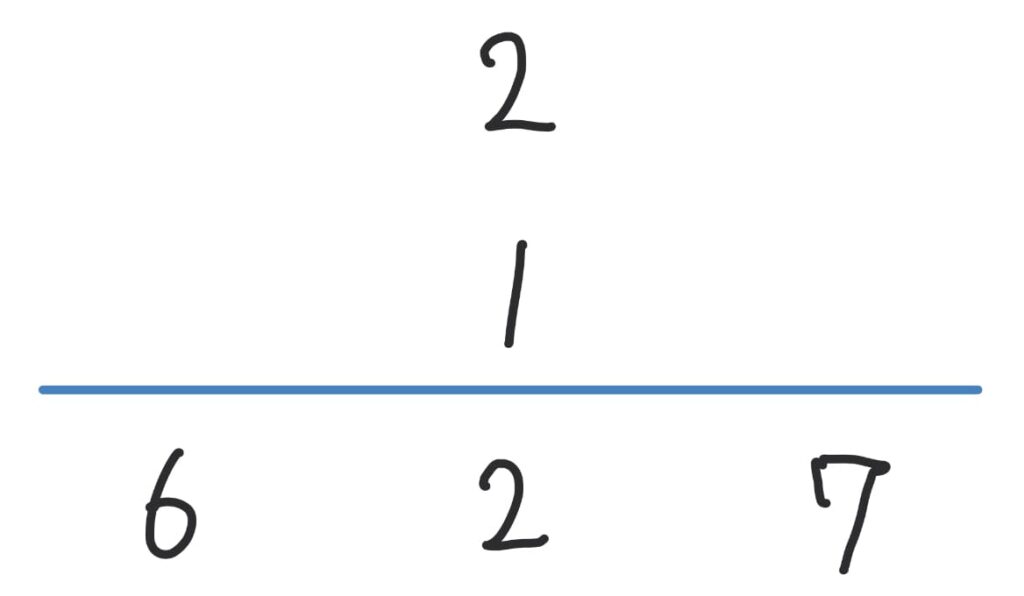
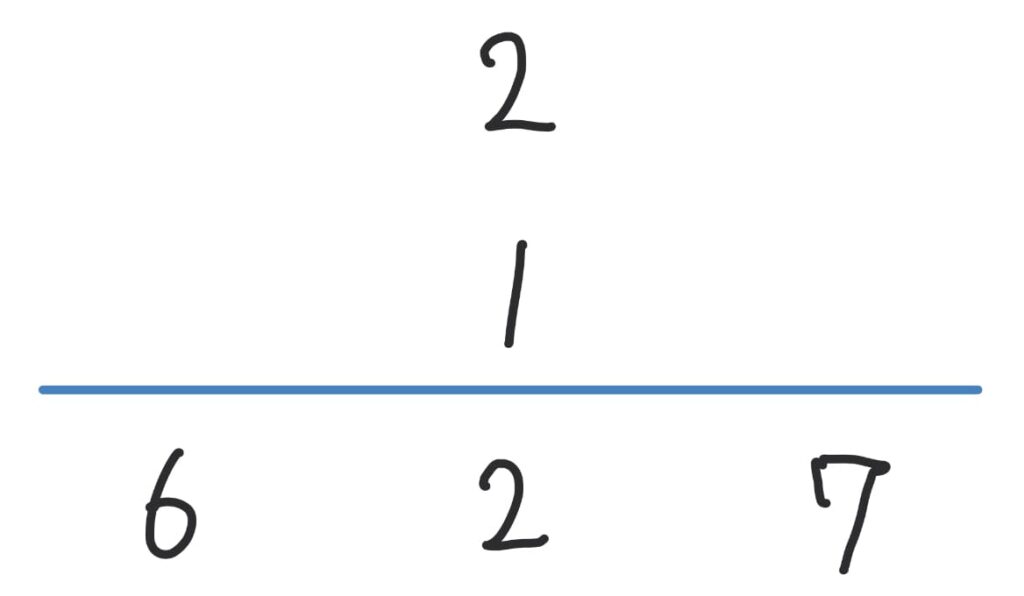
ここで迷うこととして掛けて6になるのは 「1×6」「6×1」「2×3」「3×2」の4パターンあります。つまり以下の場合があるわけです。




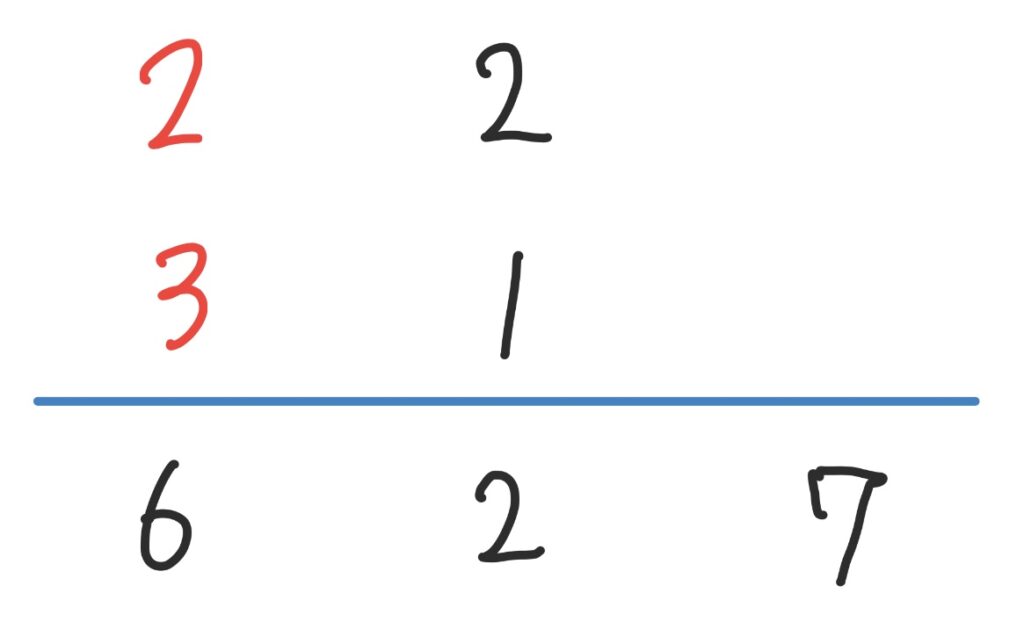
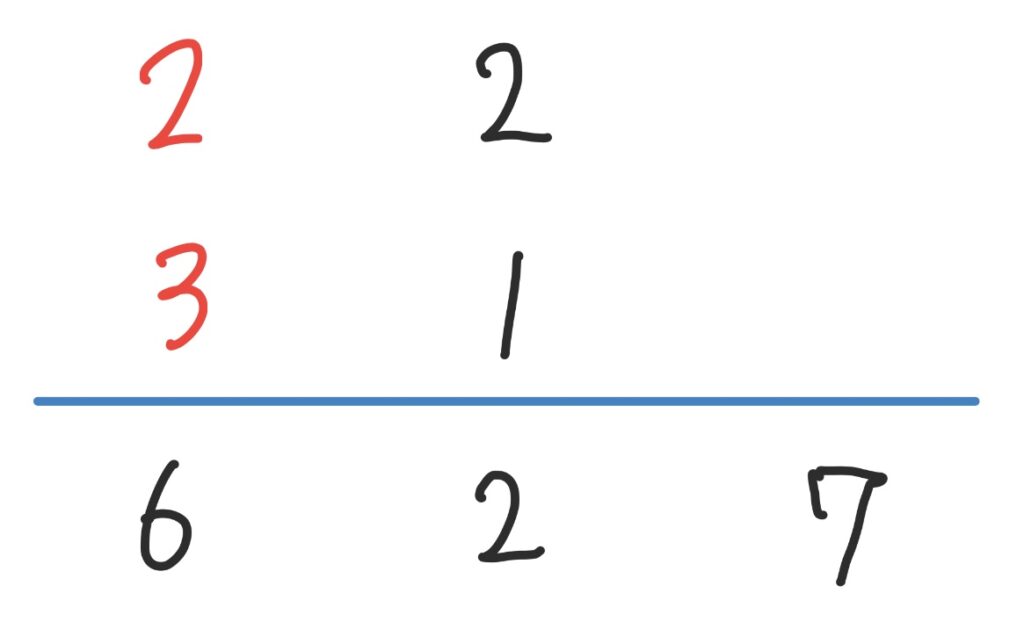
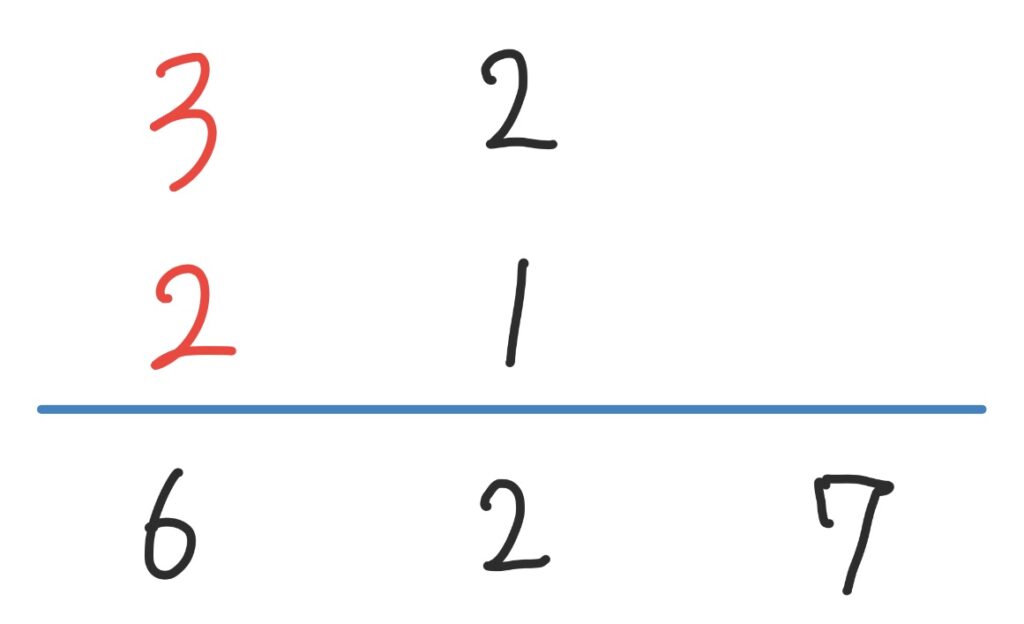

しかしここでこれから紹介する考え方を使えば2つにまで一瞬で絞ることができます。
たすき掛けが早くなる考え方
その考え方は…「隣同士に並ぶ数は互いに素」ということです。「互いに素」とは1以外の共通する約数を持たないという意味です。例えば2と5, 6と7, 10と13などが挙げられます。反対に2と6は約数2を持っていますし、3と9も3の約数を持っているので互いに素にはなりません。
そしてたすき掛けにおいて、隣に並ぶ数は必ず互いに素になります。(理由は後述)
従って先ほどの4つの中から以下の2つはまず除外できるんです。


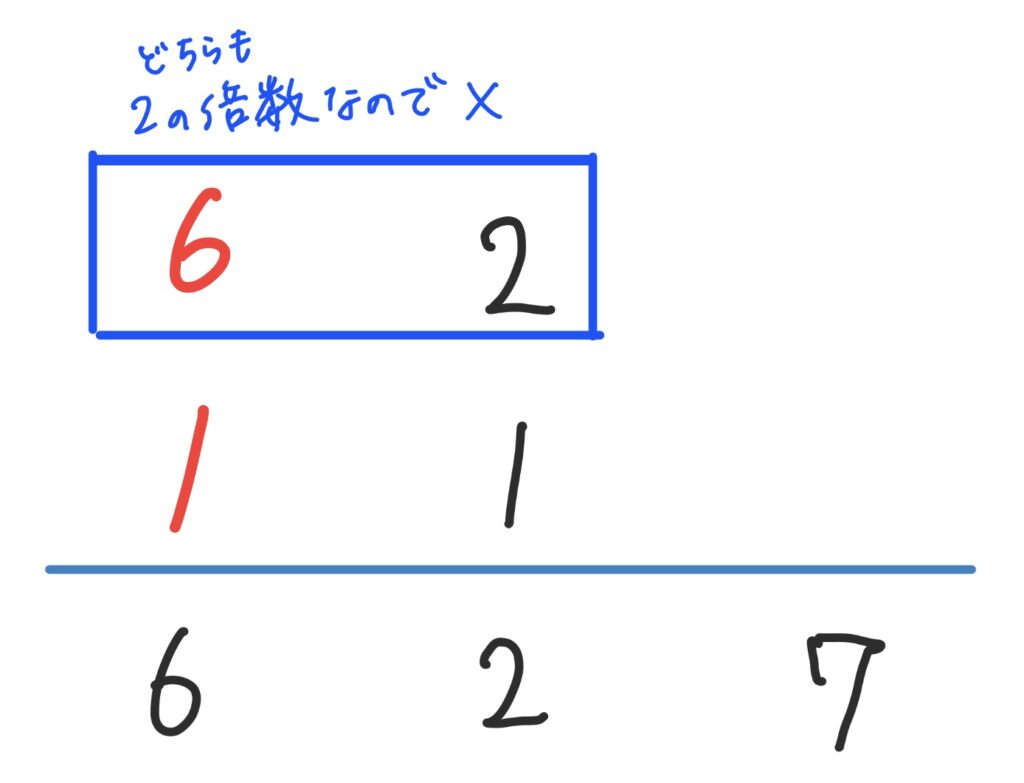

ですので後は、以下の2つを試したら良いということになりますね。経験上、掛けて6の場合は多くが「2×3」の組み合わせを選ぶと上手くいきます。今回も2つ目のパターンが正解になります。




なぜ隣に並ぶのは互いに素になるのか。
もし以下のパターンで上手くいくとしましょう。


この場合は因数分解の結果はこのようになりますよね。
\begin{eqnarray}
(6x+2)(x+1)
\end{eqnarray}
しかし前半の部分は2でくくることが出来ますよね。因数分解は基本的に共通の因数があれば括り出さなければいけません。そもそもたすき掛けをしたのにさらに数字でくくれるというのは少し変な話になってしまうわけです。
ですのでそれ以上共通因数で括ることが出来ないように、隣同士には互いに素である数を並べることになるんです。



この考え方は筆者は学校では教わらずに塾で習いました。これをご覧の中でも、気にしたことがなかったという方は多いのではないでしょうか。地味ですがスピードアップに使える方法ですので、次回から取り入れてみてくださいね。
他にYouTubeで見つけた、裏技のおすすめ動画をご紹介してこの記事は終わりにしたいと思います。ここまで見ていただきありがとうございました。勉強頑張ってください!












コメント