今回の問題
△ABCの3つの内角∠A、∠B、∠Cの大きさを、それぞれA,B,Cとするとき、次の等式が成り立つことを証明せよ。
\begin{eqnarray}
\sin \frac{A}{2}=\cos\frac{(B+C)}{2}
\end{eqnarray}
主に定期テストで問われることが多いタイプの問題です。必ずマスターしましょう!
解答例
この後に、この問題を解くための思考のプロセスを紹介していますので併せてそちらもご覧ください。
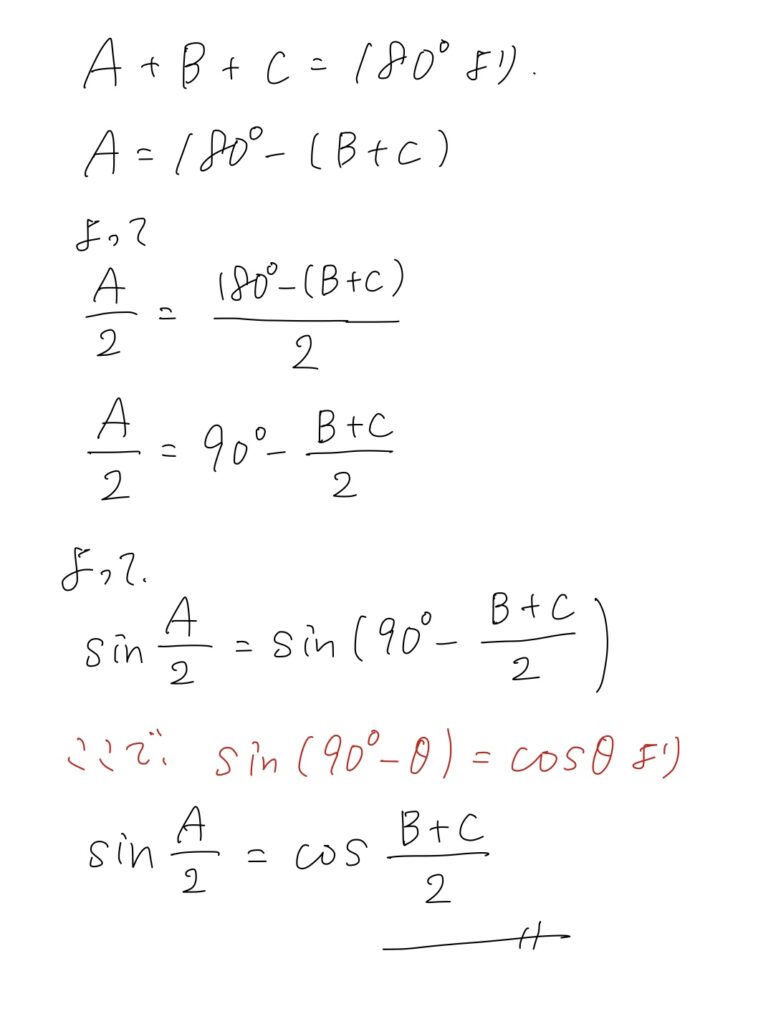
思考のプロセス
まずは証明したい式に B+C があるので、それを作ることを考えます。三角形の内角の和は180°ですので
\begin{eqnarray}
A=180°-(B+C)
\end{eqnarray}
そのあとは両辺を2で割って、さらに目的の式に近づけます。そして両辺のcosをとって問題の式にそろえます。
\begin{eqnarray}
\sin\frac{A}{2}=\sin(90°-\frac{B+C}{2})
\end{eqnarray}
ここで、
\begin{eqnarray}
\sin(90°-θ)=\cosθ
\end{eqnarray}
の関係式を使いましょう。この式は理想は暗記ではなく導出です。できなければ重要な関係式ですので、復習してください。そうすることで目的の式が証明できました。
練習問題
(1)△ABCの3つの内角∠A、∠B、∠Cの大きさを、それぞれA,B,Cとするとき、次の等式が成り立つことを証明せよ。
\begin{eqnarray}
\cos \frac{A}{2}=\sin\frac{(B+C)}{2}
\end{eqnarray}
(2)△ABCの3つの内角∠A、∠B、∠Cの大きさを、それぞれA,B,Cとするとき、次の等式が成り立つことを証明せよ。
\begin{eqnarray}
\tan \frac{A}{2}\tan \frac{B+C}{2}=1
\end{eqnarray}
練習問題の解答例
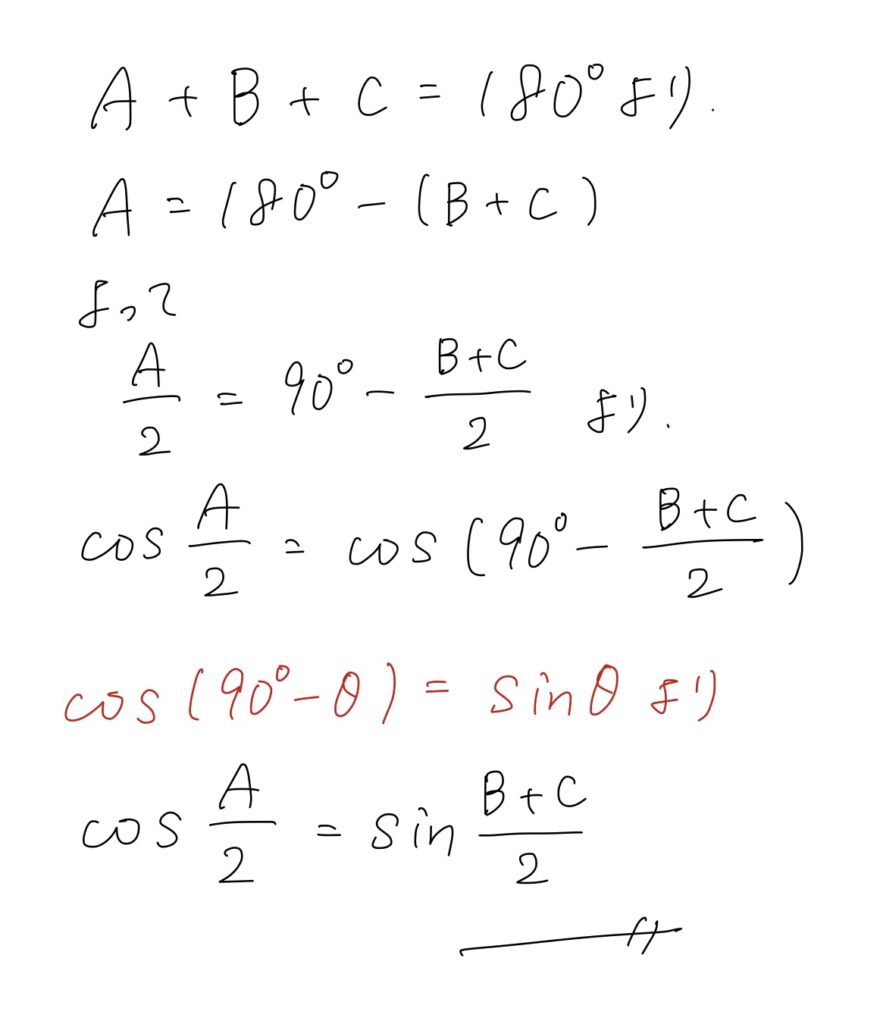












コメント