多くの方が高校1年生で学習する“チェバの定理”。教科書を見ると式の複雑さに混乱してしまう方も多いのではないでしょうか。というのも筆者もその一人でした。しかし高校の時に学んだある覚え方をすることで、それ以降簡単に解けるようになりましたので、今回の記事ではそれらを全て解説します!

この動画を見て定期テストを乗り越えましょう!!
チェバの定理とは?
まずよく教科書に書いてある定義を紹介しますね。
チェバの定理
△ABCの3頂点A, B, Cと三角形の辺上またはその延長線上にない点Oとを結ぶ直線が、対辺BC, CA, ABまたはその延長線上と交わるとき、交点をそれぞれP, Q, Rとすると
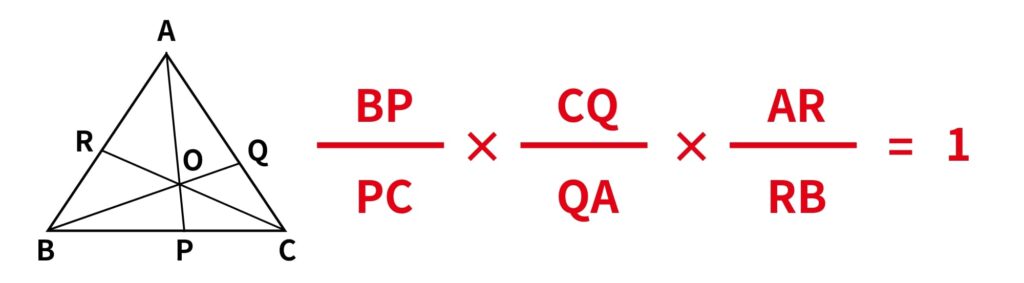

が成り立つ。
というものです。これだけだと分かりにくいですよね。これを見るだけで「難しそう…」と思うかもしれません。しかし実は、チェバの定理は覚えるためのコツさえつかめば、非常にシンプルに理解することができます!



それでは、チェバの定理を簡単に覚えるためのポイントをご紹介します!
ポイントは “3STEP”を守ること!
チェバの定理は以下の3ステップを守れば簡単に解くことができます!それぞれ詳しく解説しているので最後までご覧ください。
- 長さが分かっているところ、x,yなど文字で表されている辺を濃く書いて三角形を作る。
- できた三角形の頂点を決める。それ以外は分点とする。
- 頂点→分点はイコールの左へ。分点→頂点はイコールの右へ書く!



ひとつずつ実際に解説します!練習問題を扱いながら進めていきますね!
練習問題を使って解説!
練習問題1(交点が三角形の中にあるパターン)
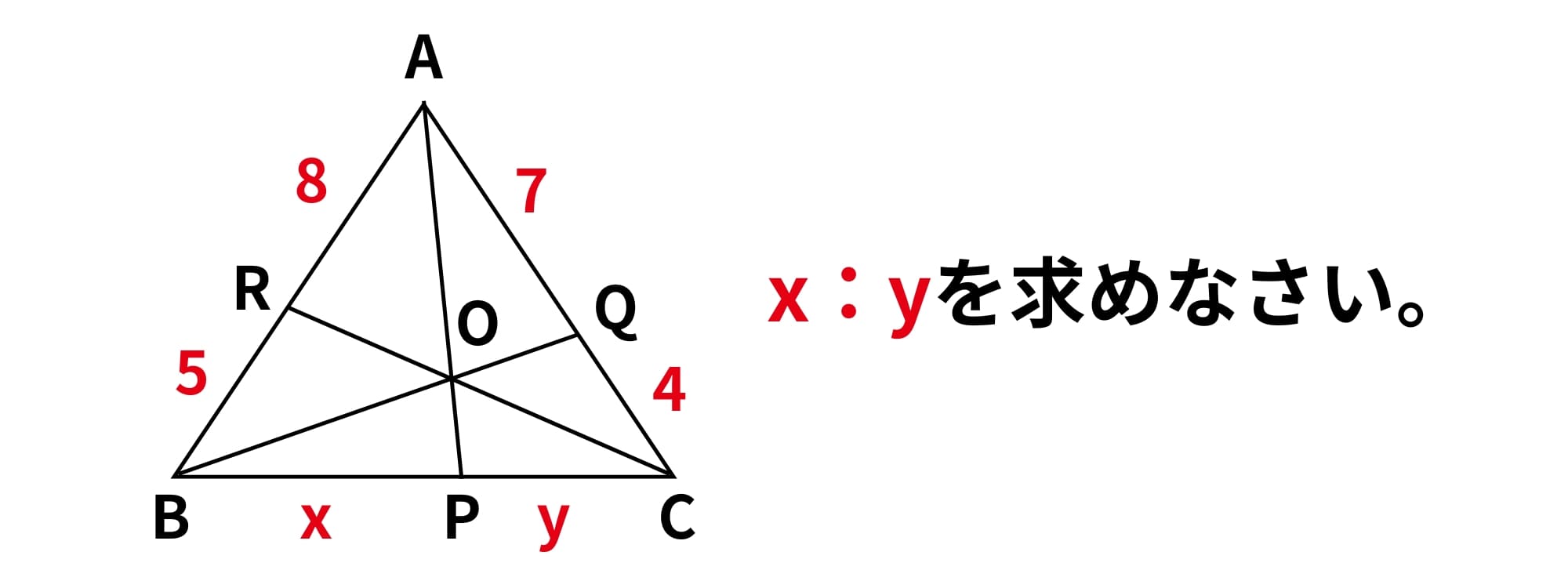

こちらの問題を使って進めていきましょう!
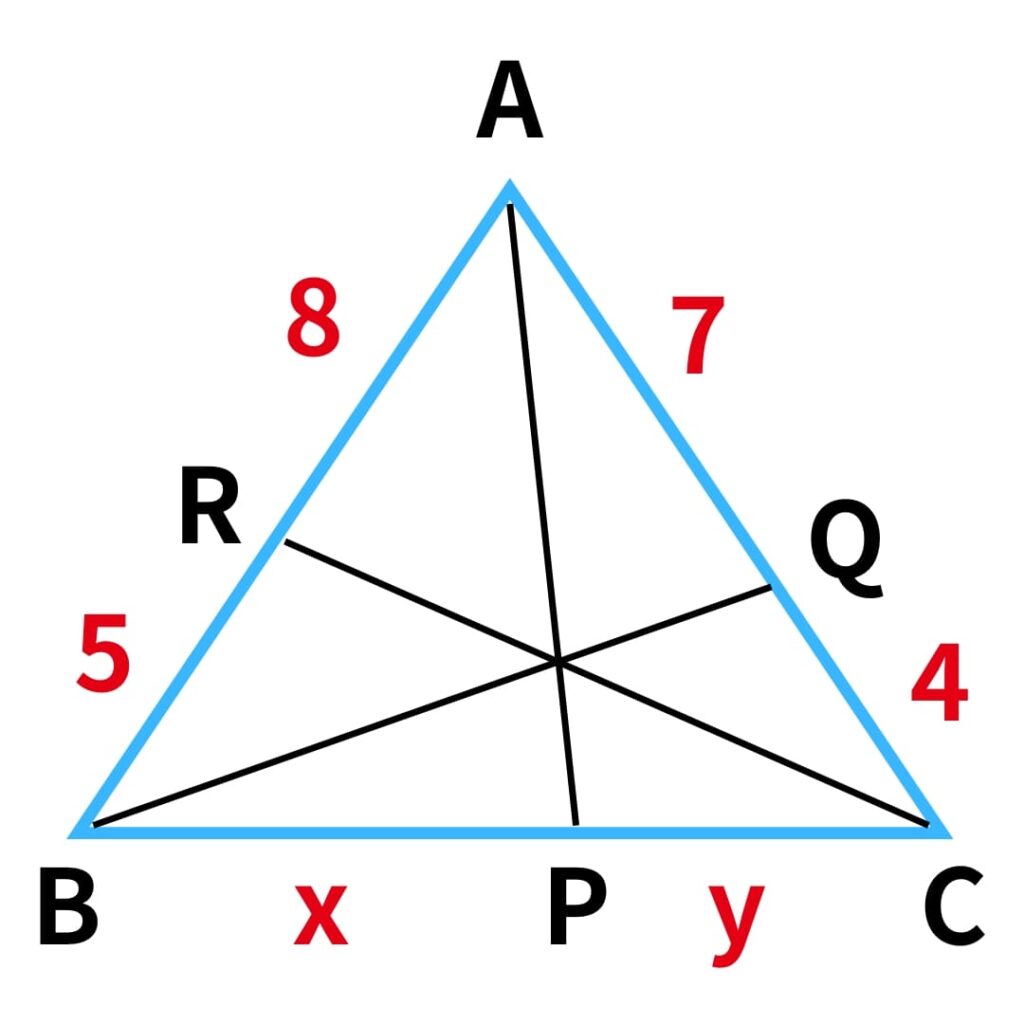

この問題で長さがわかっているところと求めたいxとyの辺を濃くしましょう。AR, RB, BP, PC, CQ, QAを濃くしたらいいですね。
そしたら今描いた線に囲まれた三角形ができますよね。今回で言うと△ABCですね。
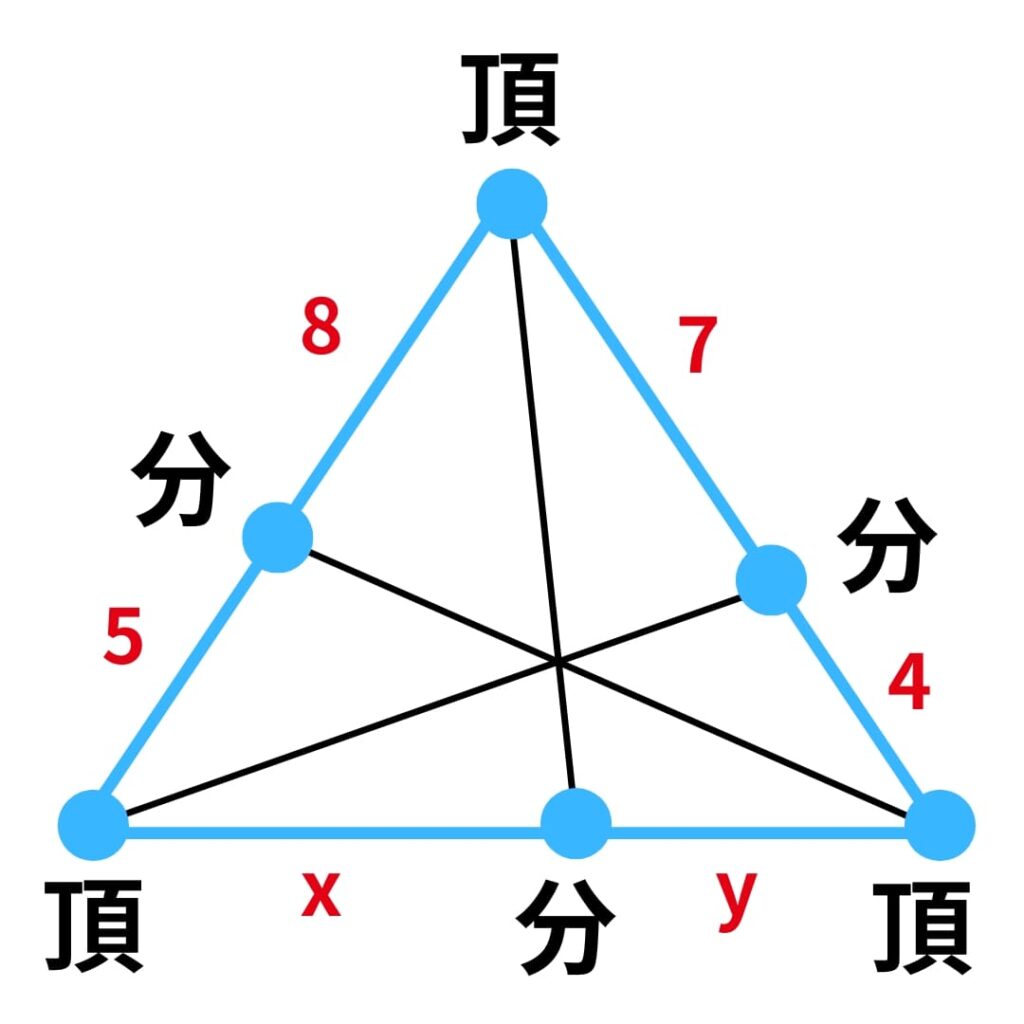

次にSTEP1で出来た三角形の頂点を決めます。今回でいうと頂点はA, B, Cのところです。またそれ以外の点は全部分点になります。
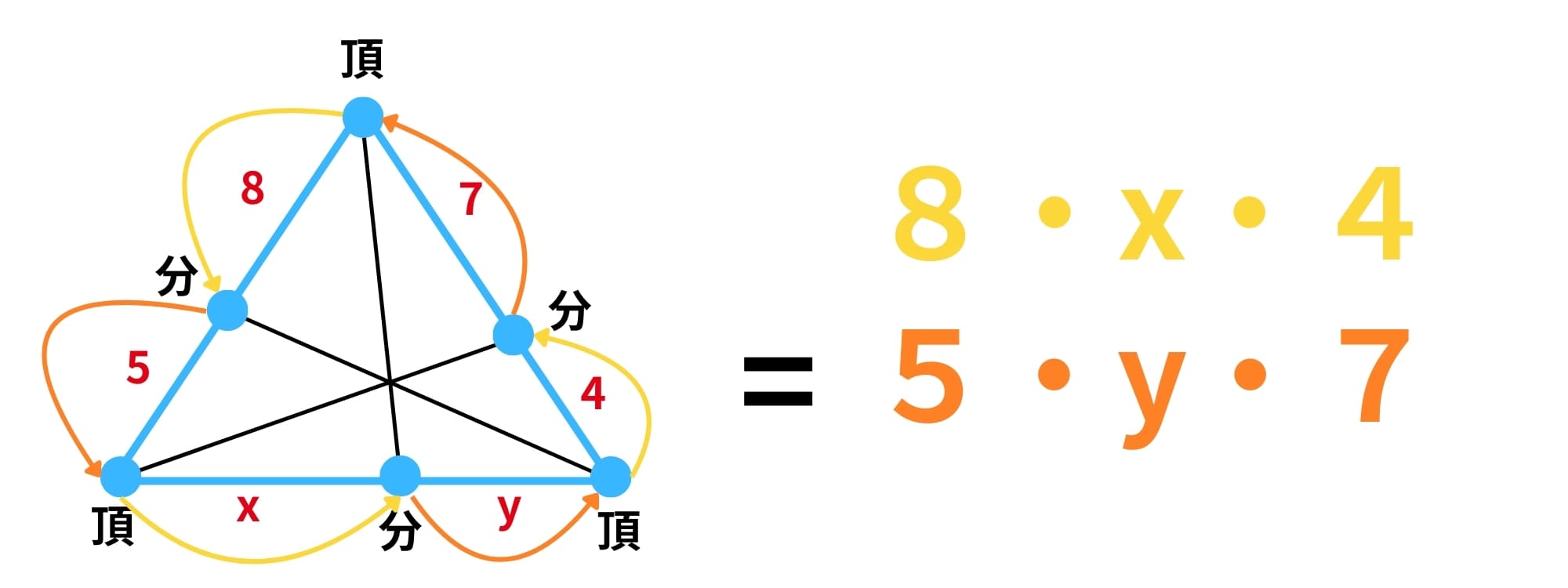

8・x・4=5・y・7と左右に分けてかけていきます!



式はこれで完成なのであとはx:yの比を計算して求めていきましょう!
三角形を1周するコツは頂点から出た矢印は必ず分点へ、分点からでた矢印は必ず頂点に向かうことです。
以下の計算はこのようになります。確認してみてください。
\begin{eqnarray}
&&8 \times x \times 4 =5 \times y \times7 \\
&&32x = 35y\\
&&x:y =35:32
\end{eqnarray}
32x : 35y から x : y = 35 : 32になるのは、内項の積=外項の積を考えると分かります。わからない方は是非調べてみてください。



これで無事答えが出ましたね!ただ、実際に手を動かしてみるとこんなことをわざわざするの…?と思いませんか?
というわけで、もう1パターンの問題を扱いつつ、この解き方の有用さに気づいていただければと思います!長くなるので次のページにまとめております👇












コメント