受験生の皆さん、勉強は順調でしょうか?受験科目の中でも数学は多くの方が苦手とする科目です。
そんな中で、もちろん正攻法を身につけるのは大切ですが…時には「ちょっとした裏技」を押さえるのがカギになることもあります。公式をしっかり覚え、その上で裏技を活用することで、時間短縮&ミス防止にもつながります。この記事では、特に役立つ10個を厳選してご紹介しますので最後まで見て覚えてくださいね!
1.2次関数の変化の割合 実用度 ★★★★★
二次関数の変化の割合は下の式で求められます。
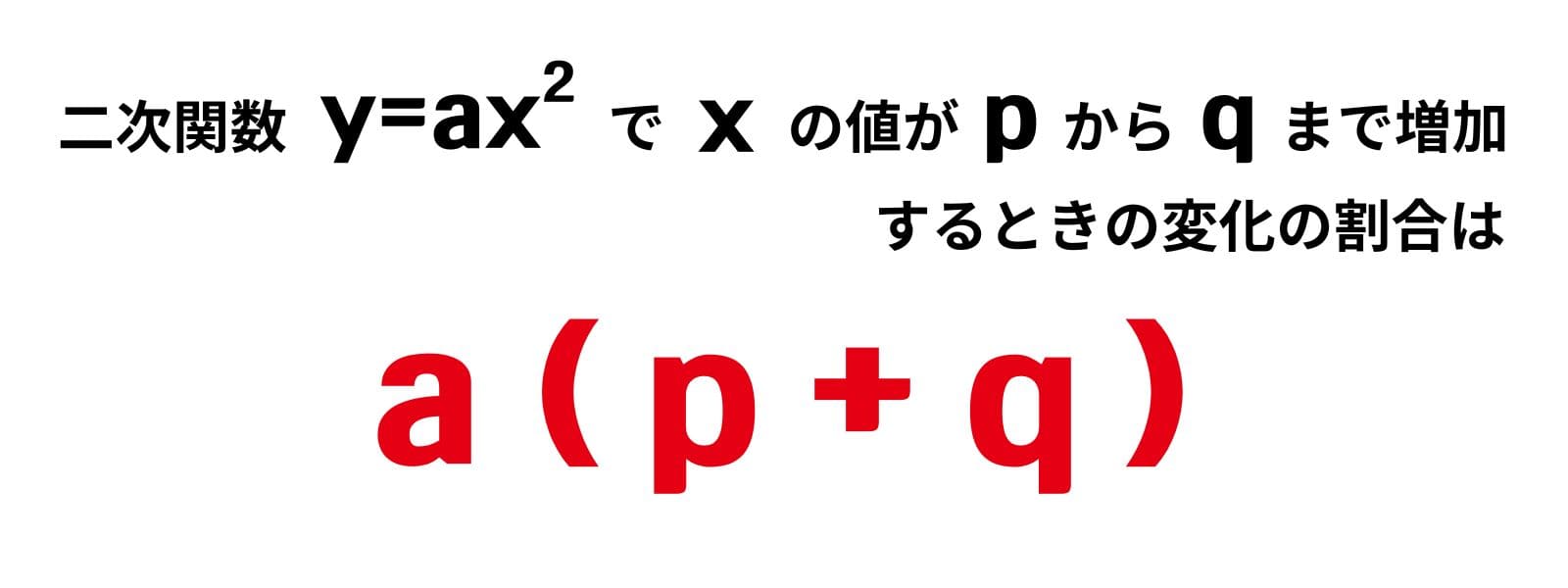
例題:y=2x2 で xの値が 3から5 に増加したときの変化の割合を求めなさい。
裏技の式に代入すると、変化の割合は 2×(3+5)=16と簡単に求められます!

数学が得意な方は、なぜこうなるのかを証明してみましょう!
xの増加量はq-pで、yの増加量はaq2-ap2となるので…?
2.2次関数と直線の交点を通る直線 実用度 ★★★★
定期テストや受験でよく問われる問題ですね。通常だったら変化の割合や連立方程式が必要になる問題ですが…?
こんな式で一発で求めることができます。文字にすると難しく感じますが、数字で試してみると案外簡単に求められますよ。
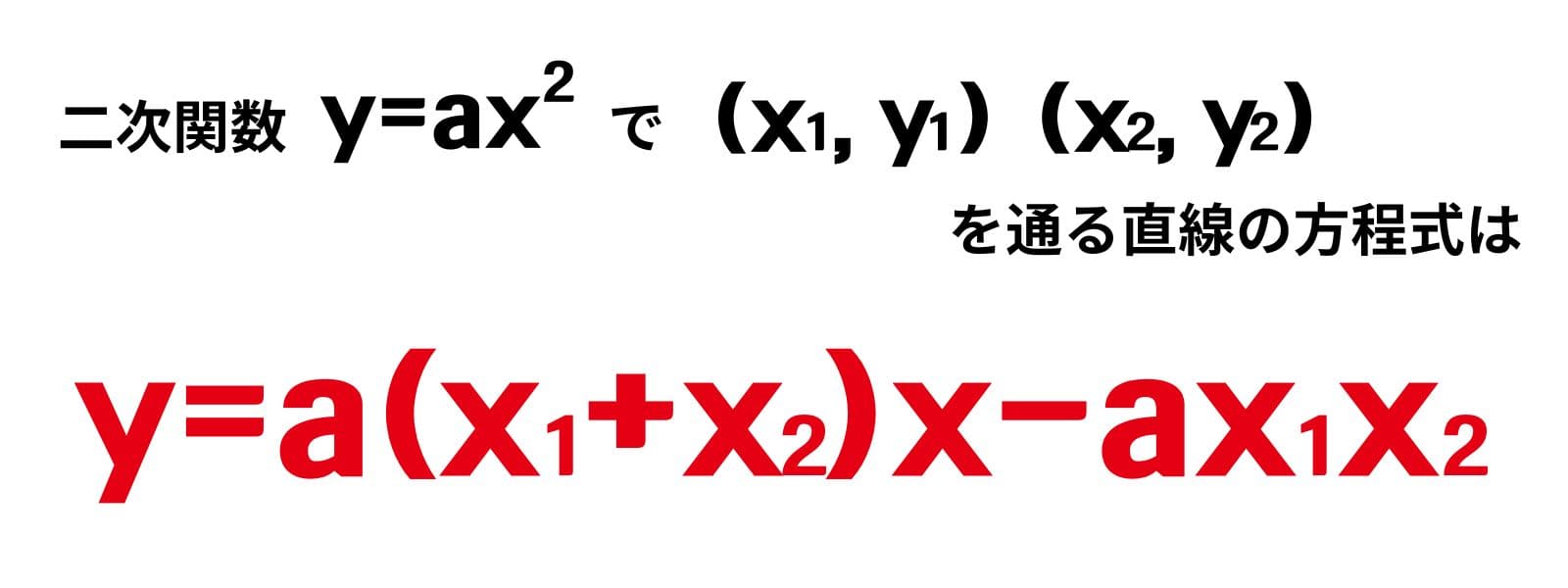
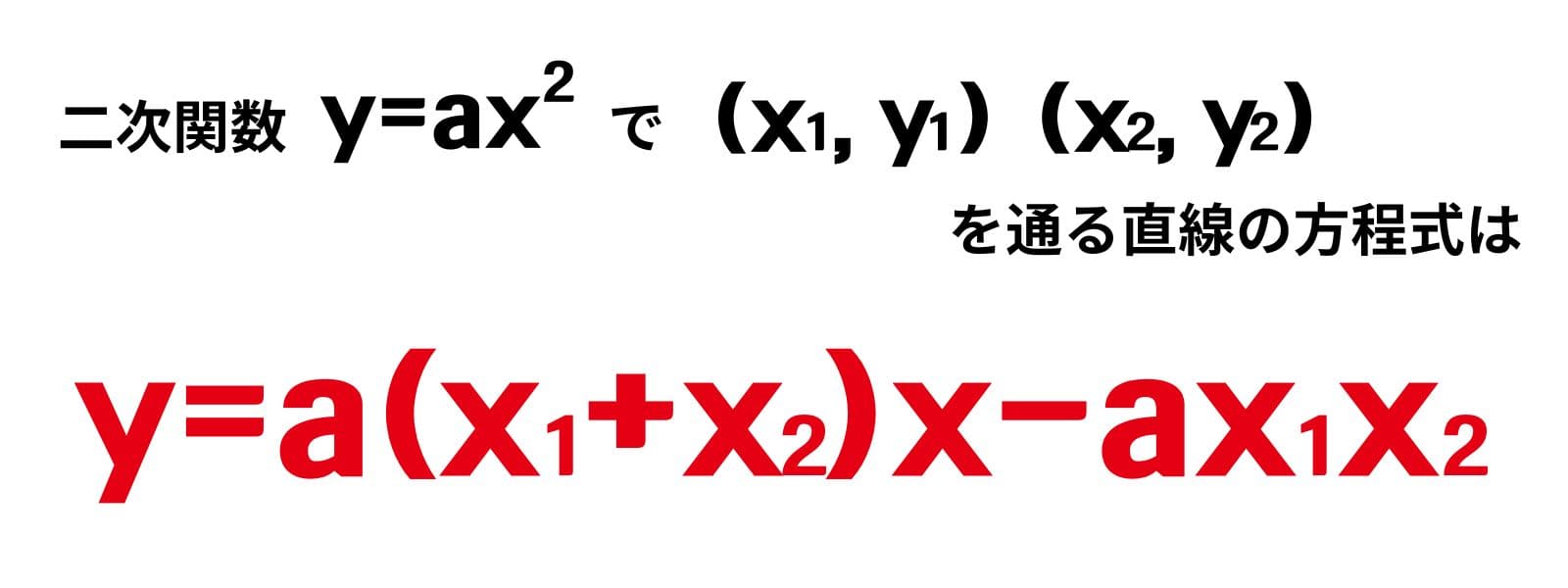
例題:y=3x2 で (-1, 3) (3, 27)を通る直線の方程式を求めなさい。
裏技の式に代入すると、y=3(−1+3)xー3×(−1)×3
つまりy=6x+9と求められますね。



なぜか知名度の低い裏技です!慣れたら本当に一瞬で式が求められます。不安な方は問題で与えられた座標を代入してみて、成り立つかどうかを確かめてみるといいですよ!
3. 分数=分数の計算方法 実用度 ★★★★★
計算をしている中で 分数=分数 の計算が出てきてどうしようと思った経験はありませんか?今日から以下の方法を使ってみてください!とても簡単に求められるようになりますよ。
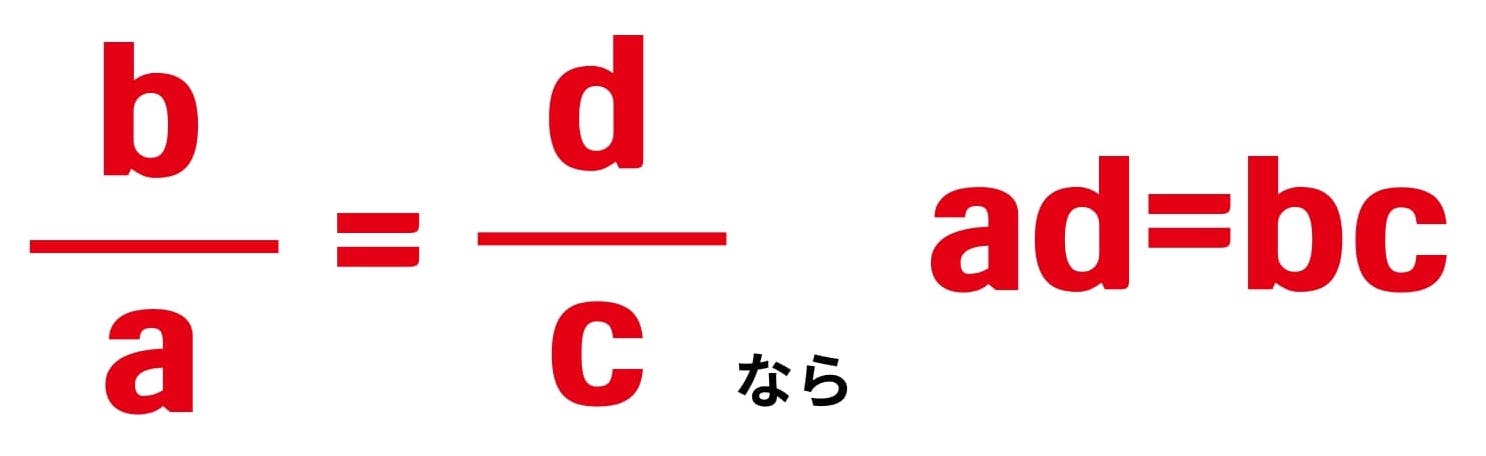

例題:
\begin{eqnarray}
&&\frac{11}{5} = \frac{x+2}{10}\\
\end{eqnarray}
斜めに掛け算して、5(x+2) = 11×10となります。あとは分配法則を使うとx=20になります。



数学だけでなく、理科の食塩水の計算などでも使える汎用性が高い裏技です。特に数学の計算が苦手な方は覚えておいて損がないです!
4. 最小公倍数と最大公約数 実用度 ★★
中学校の段階ではあまり知られていませんが、知っていると得する、痒いところに手が届く裏技です。


例題:121と1100の最小公倍数を求めなさい。
121=11×11ということに気づけたら、最大公約数が11というのが分かりますね。
したがって、ab=LGより、121×1100=11×G となります。これを解いて12100と求められます。



筆者もたまーにしか使いませんが、知っていた時のスピード差が大きいなと感じることがあるので、ここで紹介させていただきました!
5. 正三角形の面積 実用度 ★★★★
平面図形、空間図形で問われることがある正三角形の面積。これは三平方の定理を使い求めますが、ちょっと時間が掛かります。以下の式を覚えておくといいですよ。もちろん検算としても役立ちます。
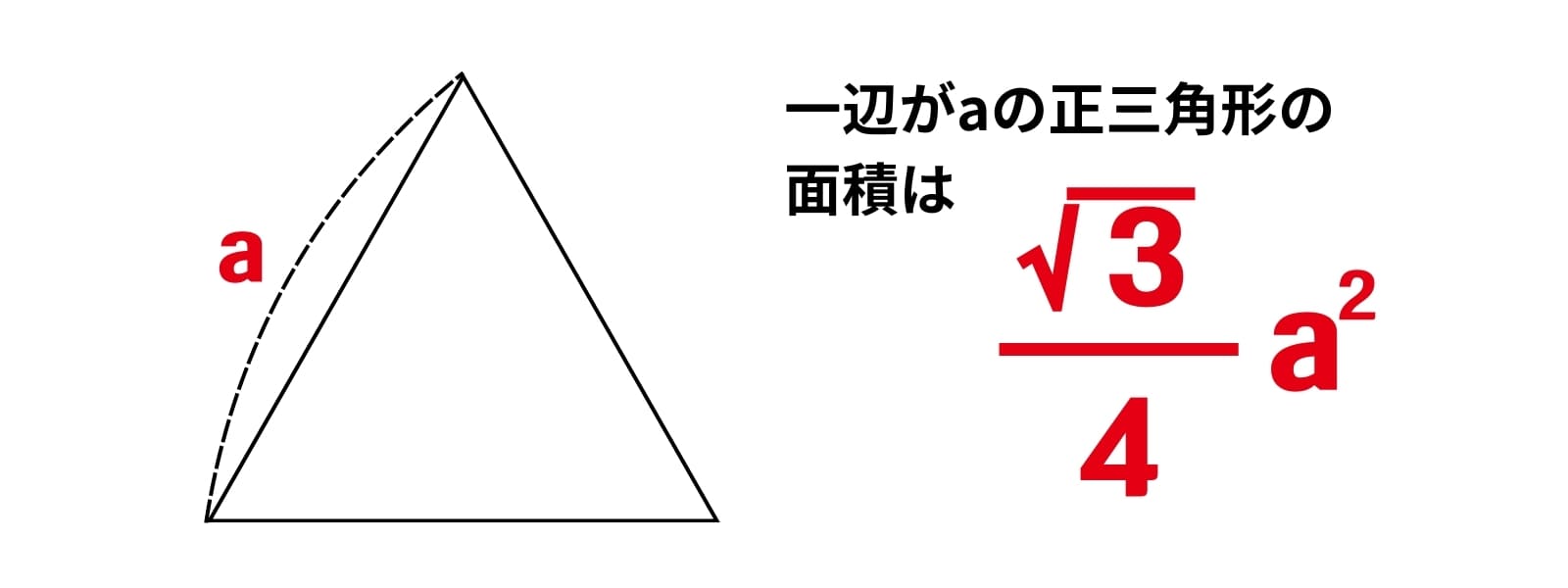

例題:1辺の長さが2の正三角形の面積を求めなさい。
裏技の公式を使いましょう。aに2を代入して、答えは√3になりますね。



「正三角形の面積を求めなさい」という問題も勿論想定はされますが、筆者の経験上、角錐の体積を求めるときの底面積の計算でよく使うイメージです!かなり時短になりますよ!



ちなみに正三角形の高さは √3a/2になりますよ。
6. 正四面体の面積 実用度 ★★★
正三角形の面積と同様のシリーズです。合わせて覚えておくといいでしょう。
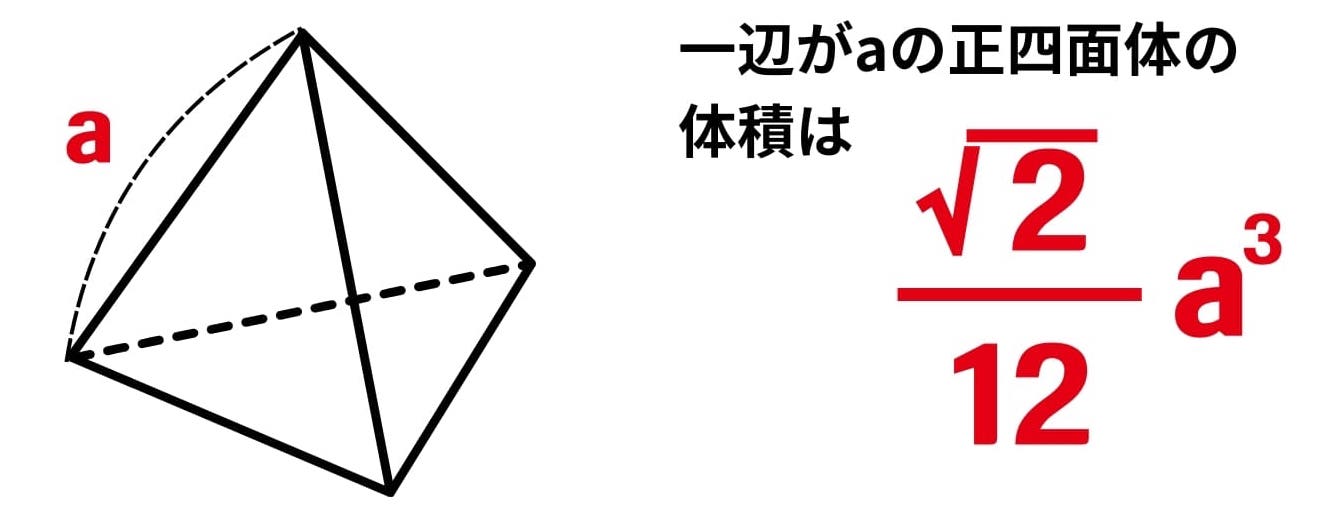

例題:1辺の長さが12の正三角形の面積を求めなさい。
裏技の公式を使いましょう。aに12を代入して、答えは144√2になりますね。



この辺りは正攻法を覚えておくことが非常に大切です!裏技に頼りすぎて応用が効かなくなることは避けてくださいね!
7. 相似を利用した問題 実用度 ★★
定期テストでもよく出題される問題。1度は解いたことがある受験生は多いでしょう。通常なら相似の性質を2箇所で使用することになります。少々難しい問題ですが、裏技で簡単に解くことができます。
ただし正攻法も経験して解けるようにしておいてくださいね。
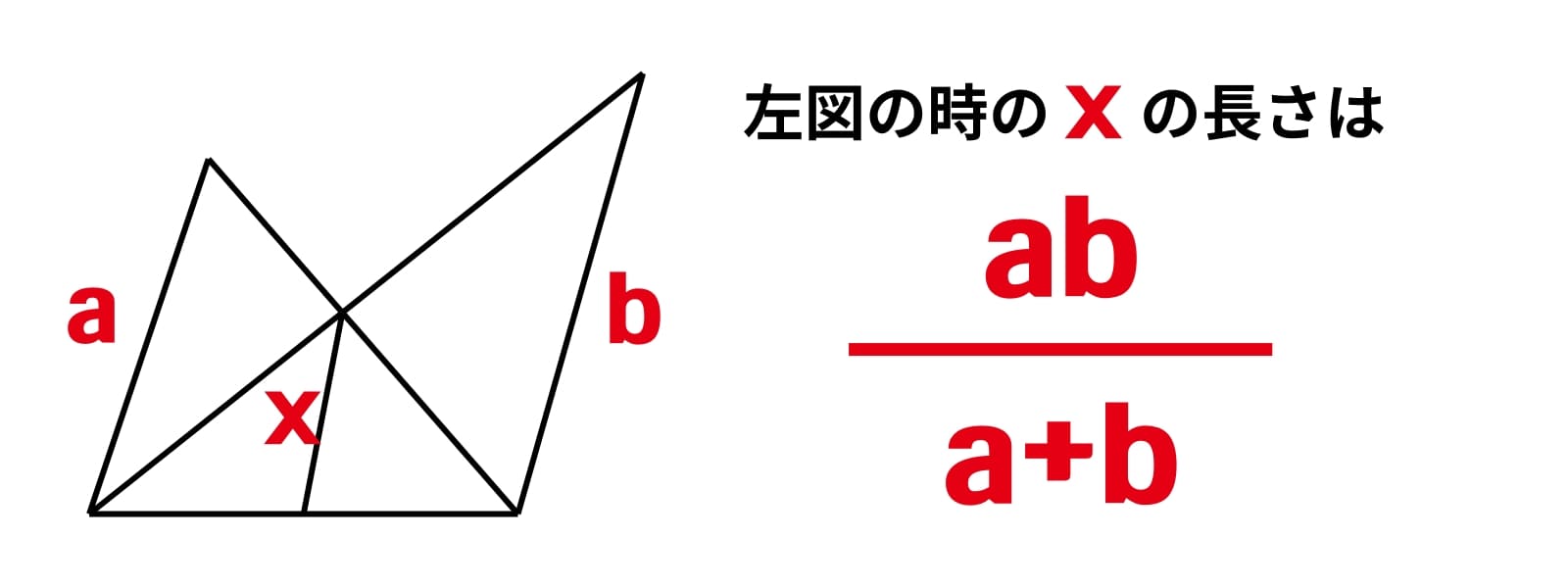

例題:
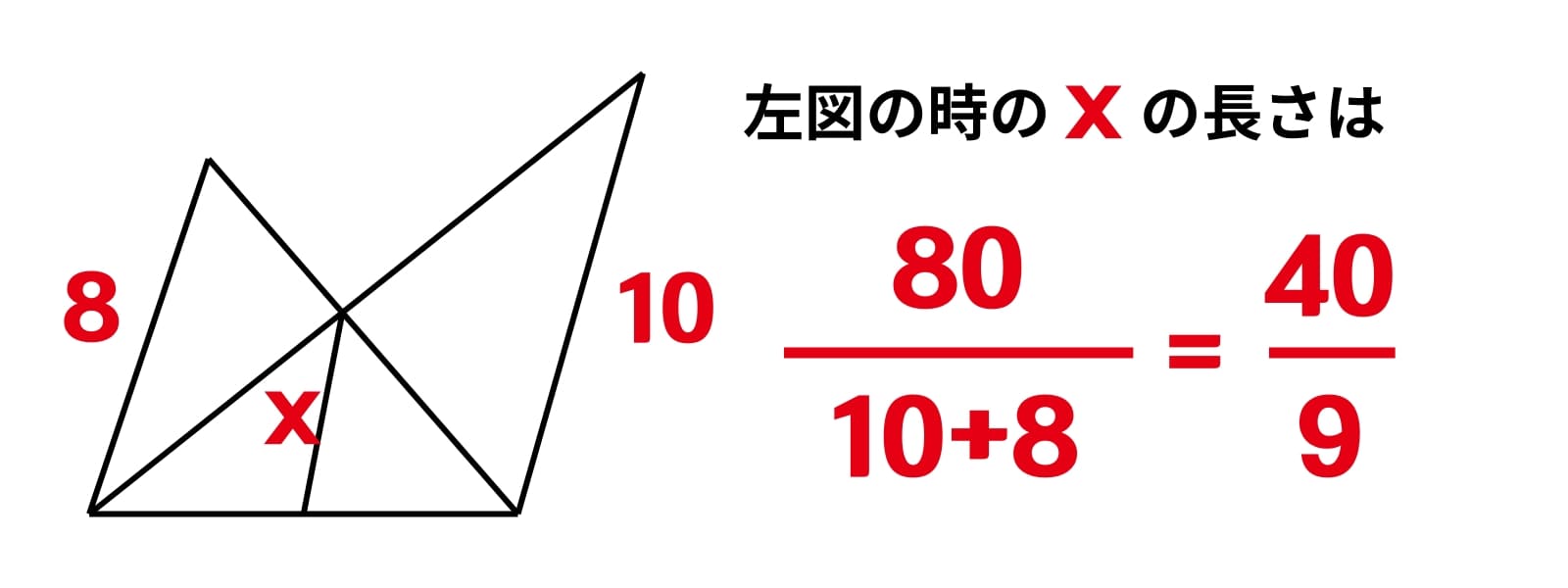




★2としたのは、使われる場面がかなり限定されているからです。ただし、この積/和というのは、理科の並列回路の合成抵抗の求め方と同じです。知らない方は調べてみてください!
8. 1の位が5の平方 実用度 ★★★★★
15、25、85など、1の位が5である数の2乗は簡単に暗算できます。使う頻度が非常に多いので、これを機にぜひ覚えてください。
◯52=◯ ×( ◯+1 )25
となります。下2桁は必ず25になります。そしてその上の位の数は◯とその次の数をかけた数字になります。
具体例で見てみましょう。
152=225(まず下2桁は必ず25。100の位は1×2)
352=1225(まず下2桁は必ず25。100の位は3×4)
752=5625(まず下2桁は必ず25。100の位は7×8)
1252=15625(まず下2桁は必ず25。100の位は12×13)



いろんな分野で使うテクニックです!是非覚えておいてほしいです!
9. 円錐の側面積、表面積 実用度 ★★★★★


となります。本来なら展開図を描いておうぎ形の面積を求めて…と手順が多いです。しかし上記の公式を使えば一瞬で求めることができますよ!
例題:次の円錐の側面積、表面積を求めよ。





底面積は円なので9πとすぐ求まりますね。確かに側面積の24πと合わせたら33πになっています!
10. おうぎ形の中心角、面積 実用度 ★★★★★
続いてはおうぎ形の紹介です!
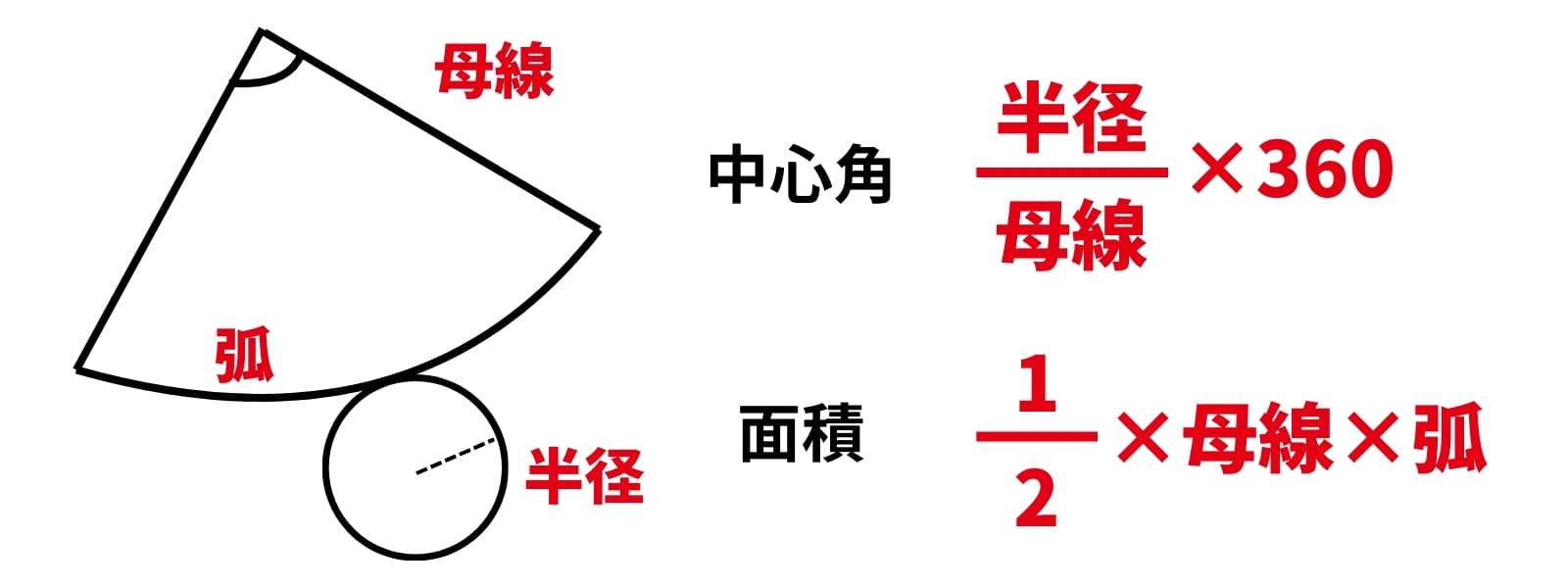

例題:次のおうぎ形の中心角、面積を求めよ。
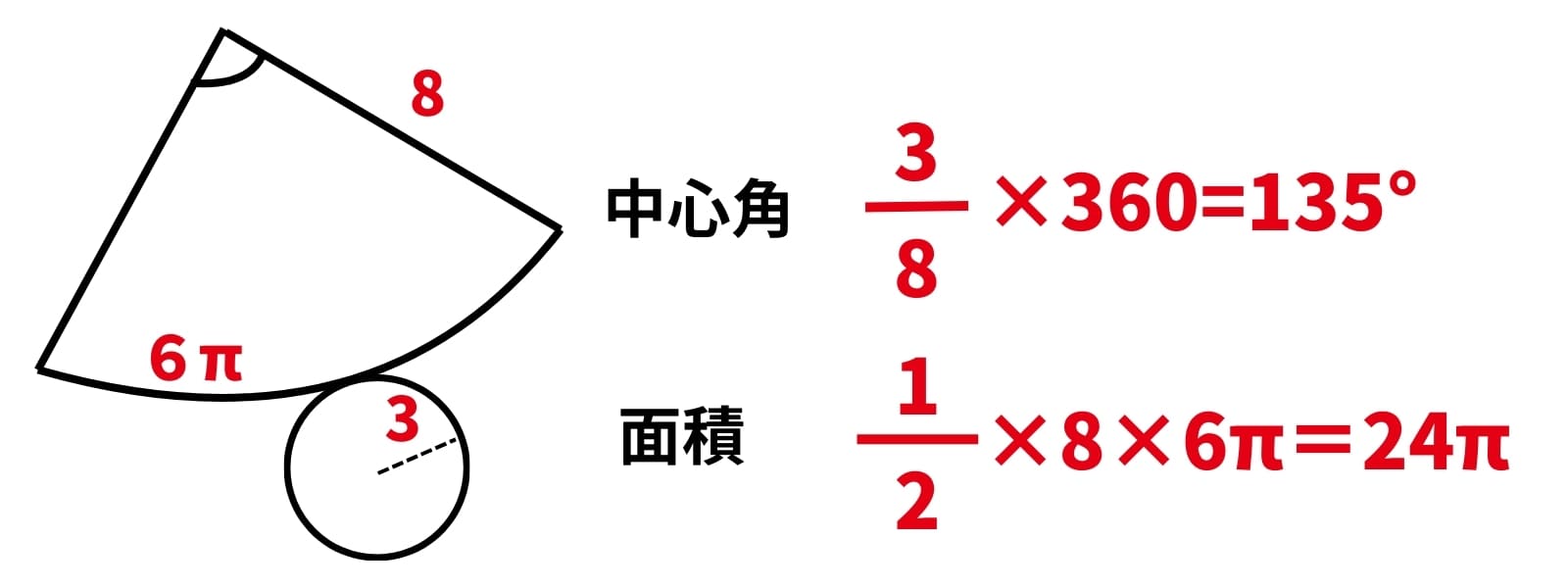




本当に色々なところで使うので、是非覚えておいてくださいね!
以上になります!今後も随時追加していく予定です!このサイトでは学生の皆さんに有益な記事を多数あげておりますので、是非他の記事もチェックしてみてくださいね!












コメント