【いつ習う？】数学で登場する “!” (ビックリマーク)とは？階乗の意味や由来、計算方法をご紹介します。

2024年6月18日2024年12月6日

みなさん、数学の授業で突然『！』というビックリマークを見て不思議に思ったことはないでしょうか。実はこれ、数学では特別な意味を持っているんです。最初は戸惑うかもしれませんが、慣れると案外簡単に使えます。

この記事では、そんな数学のビックリマークの正体と、その使い方を分かりやすく解説していきます。
高校生の方が得点源にできるように、とても詳しく解説します！

どんなレベル帯の方にも楽しんでいただけるように準備していますので、是非最後までご覧ください！

この記事の目次

【！】は「階乗（かいじょう）」という

では、数学におけるビックリマークの正体を解き明かしていきます。このビックリマーク「!」は、数学では「階乗（かいじょう）」と呼ばれる概念を表しています。階乗とは、ある正の整数までのすべての整数を掛け合わせたもののことです。

例えば、「５！」と書かれていたら、それは「５の階乗」を意味し、以下のように計算します。

\begin{eqnarray}
&&5!=5×4×3×2×1=120\\
\end{eqnarray}

もう少し例を挙げてみましょう。

\begin{eqnarray}
&&4!= 4×3×2×1=24\\
&&3!= 3×2×1=6\\
&&2!= 2×1=2\\
\end{eqnarray}

１つずつ数を小さくしていって、１になったら終わりなんですね！

お気づきかもしれませんが、階乗は数が大きくなるにつれて急激に値が大きくなります。例えば

\begin{eqnarray}
&&10!= 3628800\\
&&13!= 6227020800\\
\end{eqnarray}

といった具合に爆発的に大きくなっていきます。

後ほど、「100！は末尾に何個の０が並ぶか？」という問題についても扱います！是非このままご覧ください。

階乗はいつ習う？

階乗は高校数学の「数学A」で習い、文理問わず高１で学習します。

中学２年生で確率を習いますが、その時に一部学習するところもあるようですね！教える先生による違いが大きそうです！

【！】を使った練習問題

1. KAIJOU という６文字を並び替えてできる文字の組み合わせは全部で何通りあるか？

例えば、”JAKIOU” “OAIUKJ”などなど…たくさんありますね。こんな考え方をしてみましょう。

箱を全部で６つ用意します。その箱の中にアルファベットを１つずつ入れていくことにします。この時、１番左に入るのはK,A,I,J,O,Uの６通りです。

そして次の箱は、一番左の箱に入ったアルファベット以外なので、５通りあります。

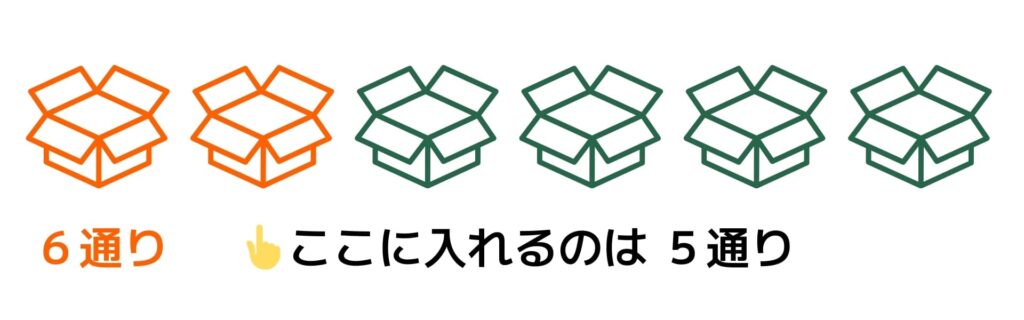
この操作を続けると、以下のようになります。つまり左から、６通り、５通り、４通り、３通り、２通り、１通りとなります。

よって、積の法則より、６×５×４×３×２×１＝７２０通りが答えです。この計算はまさに６！そのものですね。

ポイント

異なるn個のものを並べる時の並べ方は n！通りある。

2. EXPERIENCE という１０文字を並び替えてできる文字の組み合わせは全部で何通りあるか？

先ほどと同様の問題ですね。同じ解き方をすると、１０！＝３６２８８００通り　と求められそうですが、１つ落とし穴があります。下図のように、Eはどこにあっても変わらないですよね。

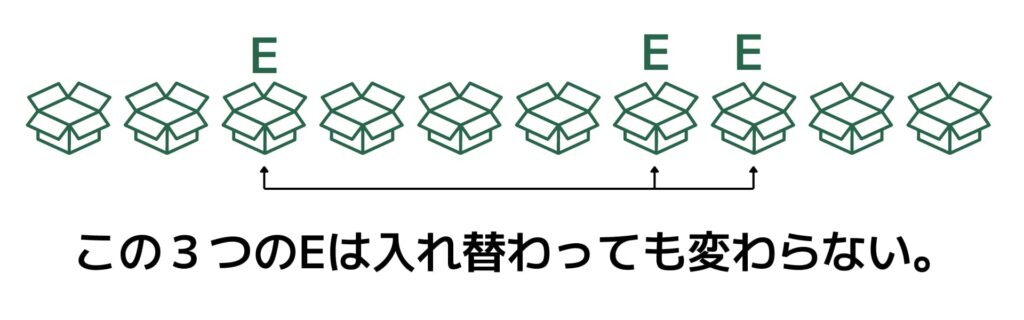
この３つのEがバラバラだったら、３！＝６通りの並べ方が生まれていたはずですが、今回はないため、１０！÷３！＝６０４８００通りが答えです。

よくある誤答として、１０！ー３！という回答を見かけます。３！通りに対して、それぞれアルファベットの並べ方があるので、今回は割り算になりますね。

100！は末尾に何個の０が並ぶか？

こちらも有名問題です。高校生は必ずマスターしておきたいです。まず問題の意味から、「末尾に何個の０が並ぶか」ということですが、例えば、32000だったら３個。100900だったら２個ですね。この末尾の０の数は何によって決まるでしょうか。

末尾に０が１個あるごとに、１０で割れる！
０が２個あったら、１０で２回割れるし、０が３個あったら、１０で３回割れる！

正解です！
つまり、１００！が１０で何回割れるかを調べたらいいですね。

では「１０で何回割れるか」はどうしたら分かるでしょうか。少し考えてみてください。

１０は分解すると２×５となりますよね。つまり１回１０で割れる、ということは２と５を１つずつ持っているということです。１０！の中に含まれる２と５の数ですが、明らかに５の方が少ないですよね。（ピンとこない方は一度素因数分解をしてみるといいですよ！）つまり、１０！は５で何回割れるかを考えたらいいというわけですね。

まとめるとこうなります。

実際に１００！の中に５が何個あるのか、考えてみましょう！（回答はこの下に続く）

１００は５で何回割れるでしょうか。１００÷５で２０回ですね。つまりここまでで２０個の５があります。
しかし２５（５^２）の倍数は、５で２回割れます。そのような数は１００÷２５＝４個あります。

つまり全部で２０＋４＝２４個の５があるので、末尾には２４個の０が並ぶということが分かりましたね。

入試問題に挑戦！

次の問いに答えよ。
(１) ５！+４！+３！の値を求めよ。
(２) a≧４のとき、a !＋２は２の累乗になり得ないことを示せ。＜ 2015 鳥取大＞

まず１番から！この問題は解きたいところですね！

（１）５！+４！+３！＝１２０＋２４＋６＝１５０…（答）

続いて２番です。「〜ないことを示せ。という問題は数学Ⅰで習う、背理法を使ってみましょう。」

（２）a≧４のとき、a !＋２＝２^kとなる自然数 k が存在すると仮定する。
　　　a ! ＝２^k -２
　　　　＝２(２^k-１-１) … ①
ここで、k=１のとき、a !＝０となり , a≧４のときこの等式が成り立つことはない。
よって , k≧２を考える。２^k-１-１は奇数であるから , ① の右辺は素因数を 1 個しかもたない。
しかし① の左辺は a≧４のとき素因数 2 を 2 個以上もつ。（４＝２×２であるので）
これは矛盾しているため、仮定が間違っていることになる。
以上よりa≧４のとき、a !＋２は２の累乗になり得ないことを示すことができた。

いかがでしたでしょうか。階乗は他にもたくさんの場面で入試に出題されます。他の分野と合わせて出ることも多いので、十分に復習しておきましょう。

なぜ階乗は「！」で表すのか？

びっくりマークとしてお馴染みの記号ですが、なぜ階乗でも使うのか調べてみました。

階乗を表す記号「！」は、フランスの数学者Christian Krampによって考案されました。
クランプは研究の中で、階乗を簡単に表すために、ビックリマークを使っていました。
1808年、彼がそれを著書に記したことにより、階乗の記号として世に広まったのです。
ビックリマークを選んだ理由は、階乗がびっくりするくらい大きな数になるから、とも言われています。
NHK高校講座より

意外とシンプルな理由だったんですね！確かに階乗は文字をどんどんかけていくので、とても大きな数になるのはびっくりしますよね。